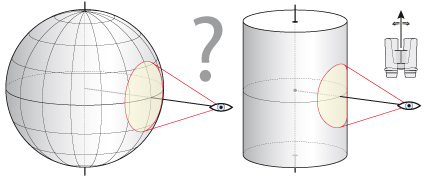
Erklärung des „Globuseffekts“, der ein Zylindereffekt ist

Warum beim Beobachten mit geschwenktem Fernglas das Bild gewölbt abzurollen scheint

Vielen Fernglasbeobachtern ist es gelegentlich aufgefallen, dass beim Schwenken des Fernglases während des Beobachtens, z.B. bei Abscannen des Horizonts oder eines Waldrandes, das Bild im kreisrunden Sehfeld des Fernglases nicht wie ein ebenes Foto, sondern wie auf einer gewölbten Fläche vorbei zu gleiten scheint. Dieses Phänomen ist seit langem unter dem irreführenden Namen „Globuseffekt“ bekannt – wahrscheinlich, weil ein Globus eine gewölbte Oberfläche hat und kreisrund wie das Sehfeld im Fernglas ist. Da jedoch nicht jeder diese Wölbung des Fernglasbildes wahrnimmt und offenbar noch niemand eine korrekte (mathematische) Erklärung für dieses unerwartete und nur während der Schwenkbewegung auftretende Verhalten geliefert hat*, wird vor allem in Fernglas- und Astro-Foren, unter Vogel-, Wild- und anderen Naturbeobachtern darüber spekuliert und gestritten.

*) Prof. Dr. Marco Pretorius schrieb in einer aktuellen Zeiss-Patentschrift u.a. dass der Globuseffekt „empirisch gut bestätigt, aber hinsichtlich seiner genauen physiologischen und wahrnehmungs-psychologischen Ursachen nach wie vor diskutiert“ werde.

Wikipedia liefert eine abwegige Erklärung, die nichts mit dem „Globuseffekt“ zu tun hat

Im Jülich-Fernglasforum stellte Dr. Holger Merlitz etwa um 2009 eine These auf, die von einer kaum bekannten, weil nur sehr geringfügigen und darum fast nur unter speziellen Testbedingungen (Schachbrettmuster) wahrnehmbaren Verzeichnung im Sehprozess von Auge und Gehirn als Ursache des „Globuseffekts“ ausgeht. Sie ist nicht nur zu gering, sondern auch weitgehend im Randbereich des Augen-Sehfeldes wirksam (das deutlich größer als der scheinbare Fernglas-Sehwinkel von etwa ±30° ist) und zudem immer und nicht nur beim Schwenken während der Fernglasbeobachtung präsent. In dieser Merlitzschen „Erklärung“ spielt weder die Schwenkbewegung noch die Fernglas-Vergrößerung eine entscheidende Rolle. Die Vergrößerung kann schon allein deshalb keinen Einfluss auf die als „Globuseffekt“-Ursache behauptete Verzeichnung haben, weil sie auf dem Informationsweg vom Objekt über das Fernglas und das Auge bis zum Gehirn zuerst im Fernglas stattfindet und erst danach im Auge-Gehirn-Komplex die Verzeichnung wirksam wird. Sie kann also den Verzeichnungseffekt weder beeinflussen noch gar verstärken. Dr. Merlitz publizierte seine abwegige Erklärung bereits 2010 unter dem Titel „Distortion of binoculars revisited: Does the sweet spot exist?“ (J. Opt. Soc. AM. A/Vol. 27, No. 1 / Jan. 2010) und er stellte sie in überarbeiteter Form vor einigen Jahren unter dem Stichwort „Globuseffekt“ auf Wikipedia ein. Sie sieht zwar wissenschaftlich aus, hat aber mit dem „Globuseffekt“ absolut nichts zu tun, wie ich schon 2009 im Jülich-Forum schrieb. Es ist nur ein Effektchen, das, sofern überhaupt bemerkt, evtl. noch hinzukommt.

Die wirkliche Ursache des „Globuseffekts“, der eigentlich Zylindereffekt heißen müsste

Beim Schwenken des Blicks ohne Fernglas oder mit einem Fernglas der Vergrößerung n = 1 scheint die beobachtete Landschaft ohne „Globuseffekt“ vorbei zu gleiten, und zwar in jedem Augenblick für sämtliche Richtungen in derselben Winkelgeschwindigkeit. Ein Fernglas mit einer Vergrößerung n > 1 vergrößert beim Schwenken die Winkelgeschwindigkeit im Fernglasbild jedoch nur für alle Bildpunkte auf der zur Schwenkrichtung rechtwinkligen Mittellinie durch das Sehfeld um den Faktor n. Dagegen bewegen sich alle Bildpunkte links und rechts davon zum Rand des Sehfeldes hin immer langsamer, bei n ≥ 8 und einem scheinbaren Sehwinkel von ±30° am linken und rechten Rand auf dem horizontalen Durchmesser abfallend auf ziemlich genau 75%. Der Grund dafür ist, dass im n-fach vergrößernden Fernglas nicht Winkel, sondern Strecken (Abstand aller Bildpunkte von der Bildmitte im reellen Zwischenbild) um den Faktor n vergrößert werden. Der Winkel vergrößert sich nur gemäß der Gleichung a' = arc tan (n · tan a).

Genau so eine Verlangsamung der Winkelgeschwindigkeit ergibt sich, wenn man auf einen um seine vertikale Achse rotierenden Zylinder schaut, und zwar im mittleren Bereich von etwa halber Zylinderbreite. Gemeinsam ist der Beobachtung mit geschwenktem Fernglas und der eines sich drehenden vertikalen Zylinders, dass sich alle über- oder untereinander auf einer senkrechten Linie liegenden Punkte mit exakt identischer Winkelgeschwindigkeit bewegen. Würde man statt eines Zylinders einen sich drehenden Globus beobachten, wäre das anders: Auf dem Äquator wäre der Winkelgeschwindigkeitsverlauf genauso wie beim Zylinder, aber darüber und darunter nähme die Winkelgeschwindigkeit ab, und zwar je näher den Polen, desto mehr. Das führte dazu, dass nur der Meridian durch die Sehfeldmitte als gerade Linie gesehen wird, alle Meridiane links und rechts davon sich zum Rand hin mehr und mehr krümmen, um genau am Globusrand zu einem Halbkreis zu werden. Sähe man im geschwenkten Fernglas tatsächlich einen „Globuseffekt“, dann hätte man eine extrem starke tonnenförmige Verzeichnung während des Schwenkens – hat man aber nicht, wenn das Fernglas orthoskopisch, also nicht verzeichnend abbildet. Die Bezeichnung „Globuseffekt“ ist somit falsch.

Um endlich Klarheit über Ursache und Wirkungsweise des irreführend als „Globuseffekt“ bezeichneten Zylindereffekts zu schaffen und den meistens ohne Fachwissen geführten Spekulationen eine mathematisch fundierte Erklärung entgegenzusetzen, habe ich einen sehr ausführlichen Beitrag „Wie der Globuseffekt entsteht und warum er Zylindereffekt heißen müsste“ verfasst. Der erste Teil soll nur anhand von logischen Überlegungen, einem praktischen Beispiel und mit anschaulichen Abbildungen auch denjenigen eine plausible Vorstellung ermöglichen, die mathematischen Berechnungen nicht folgen können. Der zweite Teil liefert dann hieb- und stichfeste mathematische Berechnungen, die von allen nachvollzogen werden können, die mit Winkelfunktionen und algebraischen Gleichungen umgehen können. Dieser mathematische Teil ist (vermutlich erstmals) eine unwiderlegbare Begründung des Zylindereffekts.

Klicken Sie auf diese Zeile, um die Zylindereffekt-Erklärung als PDF-Datei (10 Seiten) aufzurufen